Power Simulation con Gamma & Gam

Lo scenario prevederebbe un disegno fattoriale 3 (Numero di riferimento: 0, 1, 2; within-subject) × 9 (Distanza: da 1 a 9; within-subject), con numerosi trial ripetuti in ogni condizione.

Tuttavia, l’elemento di maggiore interesse, per il quale si vuole valutare la potenza, è l’effetto Distanza nel caso del numero di riferimento zero (0). Pertanto, in questa analisi ci concentreremo esclusivamente sulla simulazione in tale condizione. Si potrà poi ampliare generando le altre due condizioni e valutando l’interazione.

Inoltre, il fattore “Distanza” può essere considerato come un fattore categoriale, ma visto il numero di livelli e la correlazione tra effetti adiacenti questo rischierebbe di portare a una sovraparametrizzazione. Per evitare questo problema, proponiamo di trattare Distanza come una variabile quantitativa continua. Poiché si assume che l’effetto possa essere non-lineare, l’analisi statistica potrebbe prevedere i gam.

Pacchetti & workspace

rm(list=ls())
library(ggplot2)
library(glmmTMB)
library(mgcv)
set.seed(1006)

Definisco alcuni parametri iniziali del disegno di ricerca

Numero di livelli, osservazioni (trial), e partecipanti.

ndistances = 9 # numero di livelli del fattore Distanza
k = 40 # numero di trial per ciascun livello del fattore Distanza
N = 10 # numero di partecipanti

Stabilisco dei parametri che governano la relazione (non)lineare, che immaginiamo segmentata per semplicità. Il punto qui è generare uno scenario plausibile che potrebbe essere non lineare, e con la cui peculiare incertezza dovremo poi fare i conti (da cui i magnifici gam).

beta0 = 3 # intercetta (valore di y quando Distance = 0)
beta1 = -0.10 # slope (decremento della y per incremento unitario di Distance)
stop = 5 # dove la retta smette di scendere

Genero la componente lineare

Genero ora la componente sulla scala lineare (chiamata yLinFixed).

Distance = rep(1:ndistances, each=k, times=N)

yLinFixed = beta0 + beta1 * pmin(Distance, stop)

ggplot(data=data.frame())+
  geom_line(aes(x=Distance,y=yLinFixed),size=2)+  
  scale_x_continuous(breaks=1:ndistances)+
  scale_y_continuous(limits=c(min(yLinFixed)-0.1,max(yLinFixed+0.1)))+
  theme(text=element_text(size=25))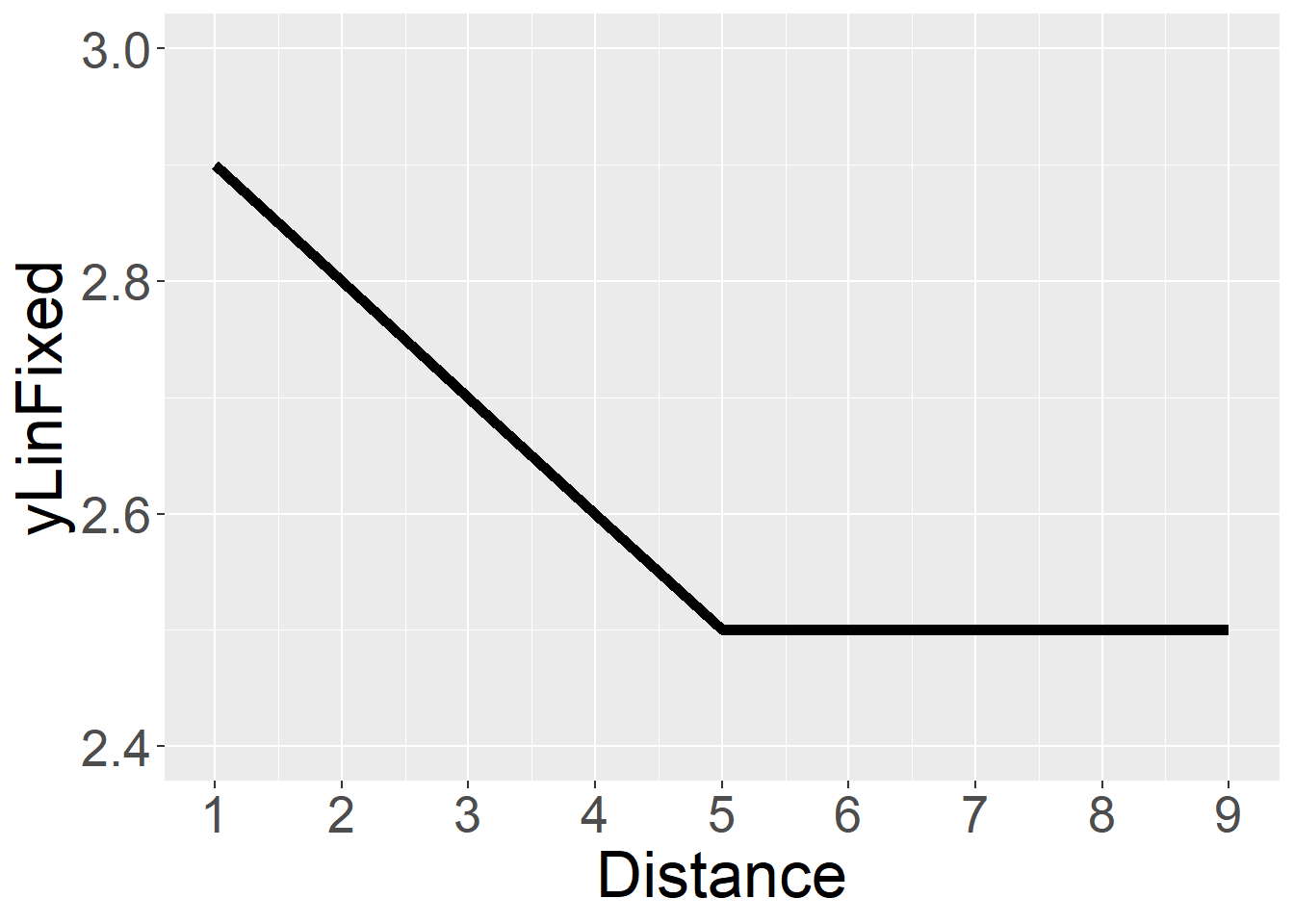

Genero i dati simulati per tutti i partecipanti

Parte random

Preparo la parte random:

id = rep(1:N,each=ndistances*k) # genero il vettore degli "id"

tauInt = 0.3 # SD dell'intercetta random
tauSlo = 0.06 # SD della slope random

rInt = rep(rnorm(N,0,tauInt), each=ndistances*k) # genero le intercette random
rSlo = rep(rnorm(N,0,tauSlo), each=ndistances*k) # genero le slope random

rStop = rep(sample(-1:1,N,replace=T),each=ndistances*k)

Componente lineare complessiva (fissa + random)

Genero la componente lineare per tutte le osservazioni e partecipanti, sommando la parte fissa e quella random:

yLin = beta0 + beta1 * pmin(Distance, stop+rStop) + rInt + rSlo * pmin(Distance, stop+rStop)

ggplot(data=data.frame(),aes(x=Distance,y=yLin,color=as.factor(id)))+
  geom_line(size=0.8)+
  scale_x_continuous(breaks=1:ndistances)+
  theme(text=element_text(size=18))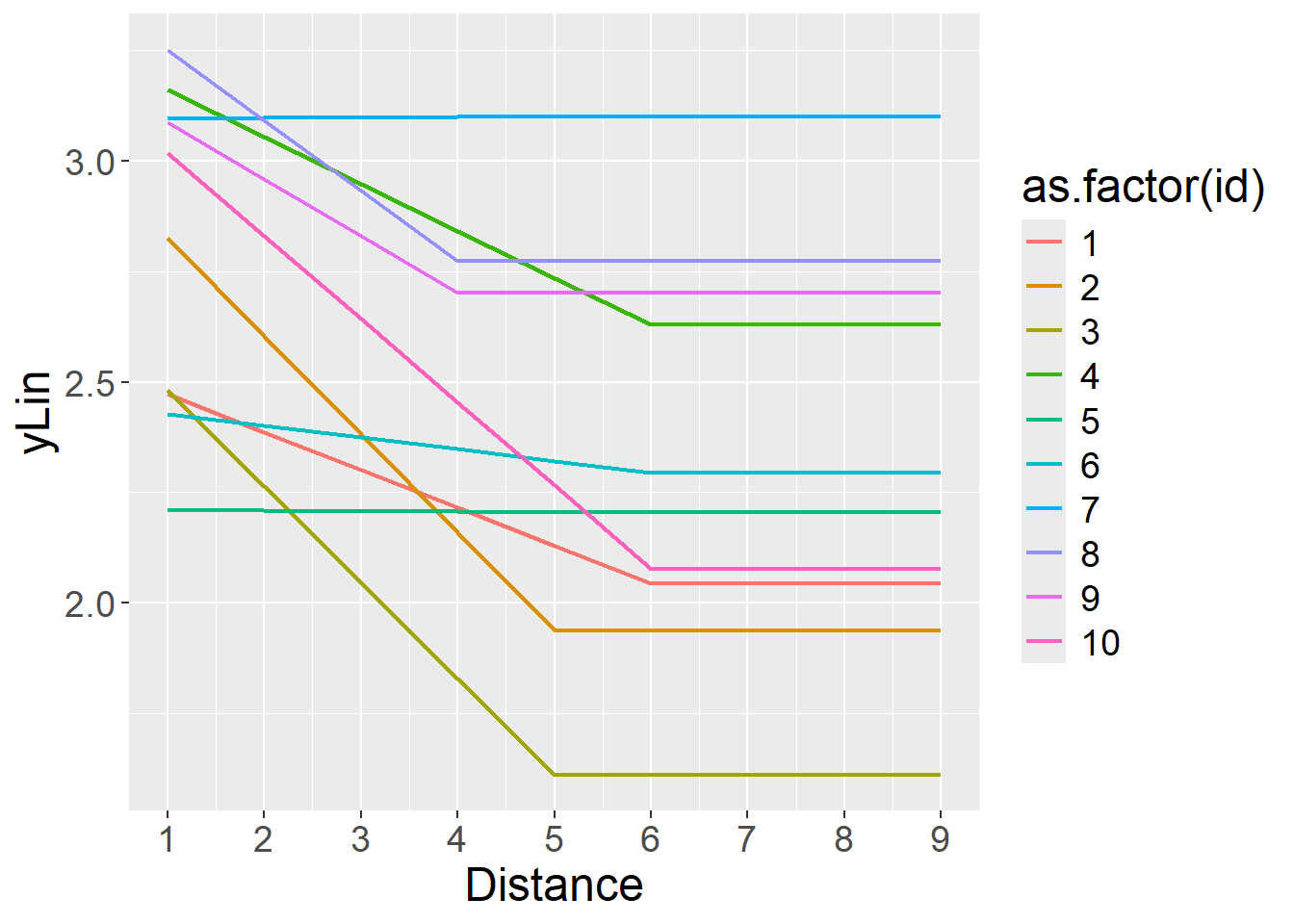

Considerata una funzione legame logaritmica, i tempi attesi dovrebbero essere questi:

ggplot(data=data.frame(),aes(x=Distance,y=exp(yLin)*30,color=as.factor(id)))+
  geom_line(size=0.8)+
  scale_x_continuous(breaks=1:ndistances)+
  theme(text=element_text(size=18))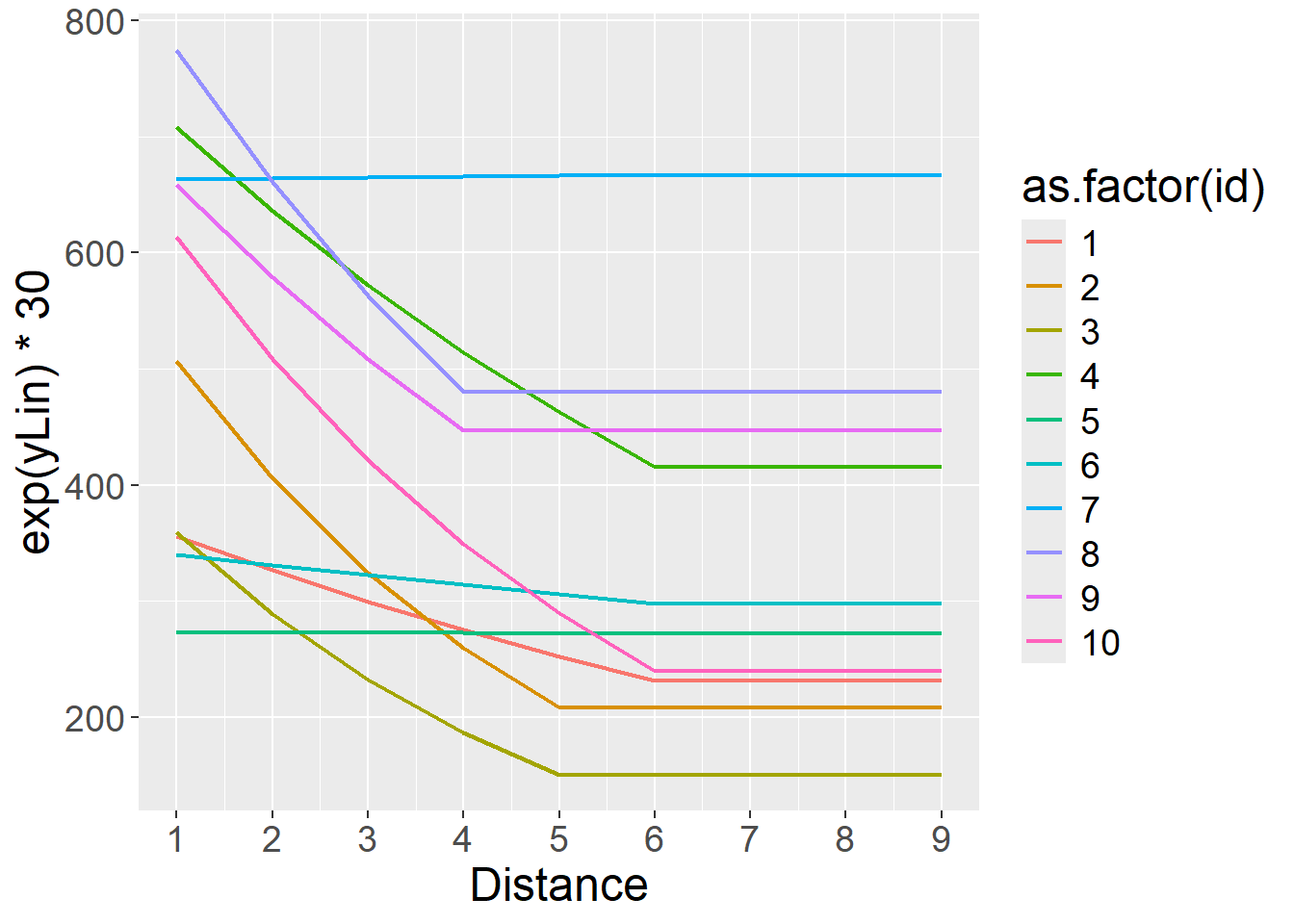

Simulazione dei Tempi di Risposta (rt)

Genero finalmente i dati simulati usando la Gamma:

rt = rgamma(N*k*ndistances, shape = exp(yLin), scale = 30)

Diamo un’occhiata ai tempi di risposta medi osservati per partecipante per condizione:

dx = aggregate(rt,by=list(id=id,Distance=Distance),FUN=median)
ggplot(data=dx,aes(x=Distance,y=x,color=as.factor(id)))+
  geom_line(size=0.8)+
  scale_x_continuous(breaks=1:ndistances)+
  theme(text=element_text(size=18))+
  labs(y="Median Response Time")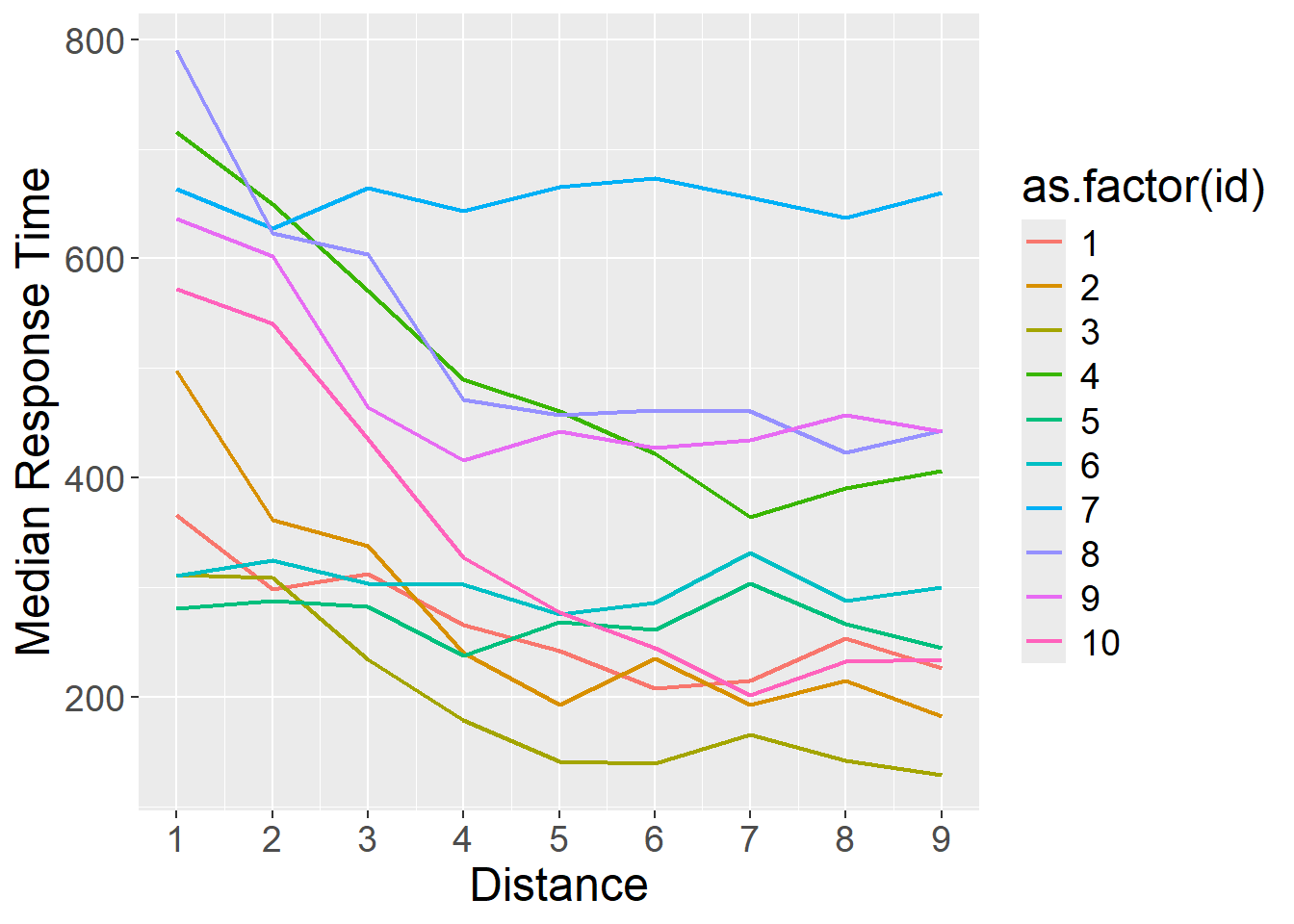

Diamo anche un’occhiata alla distribuzione complessiva dei tempi per verificare se assomiglia a quella dei tempi:

ggplot(data=data.frame())+
  geom_density(aes(x=rt,y=after_stat(density)),fill="black",alpha=.35,color=NA)+
  theme(text=element_text(size=18))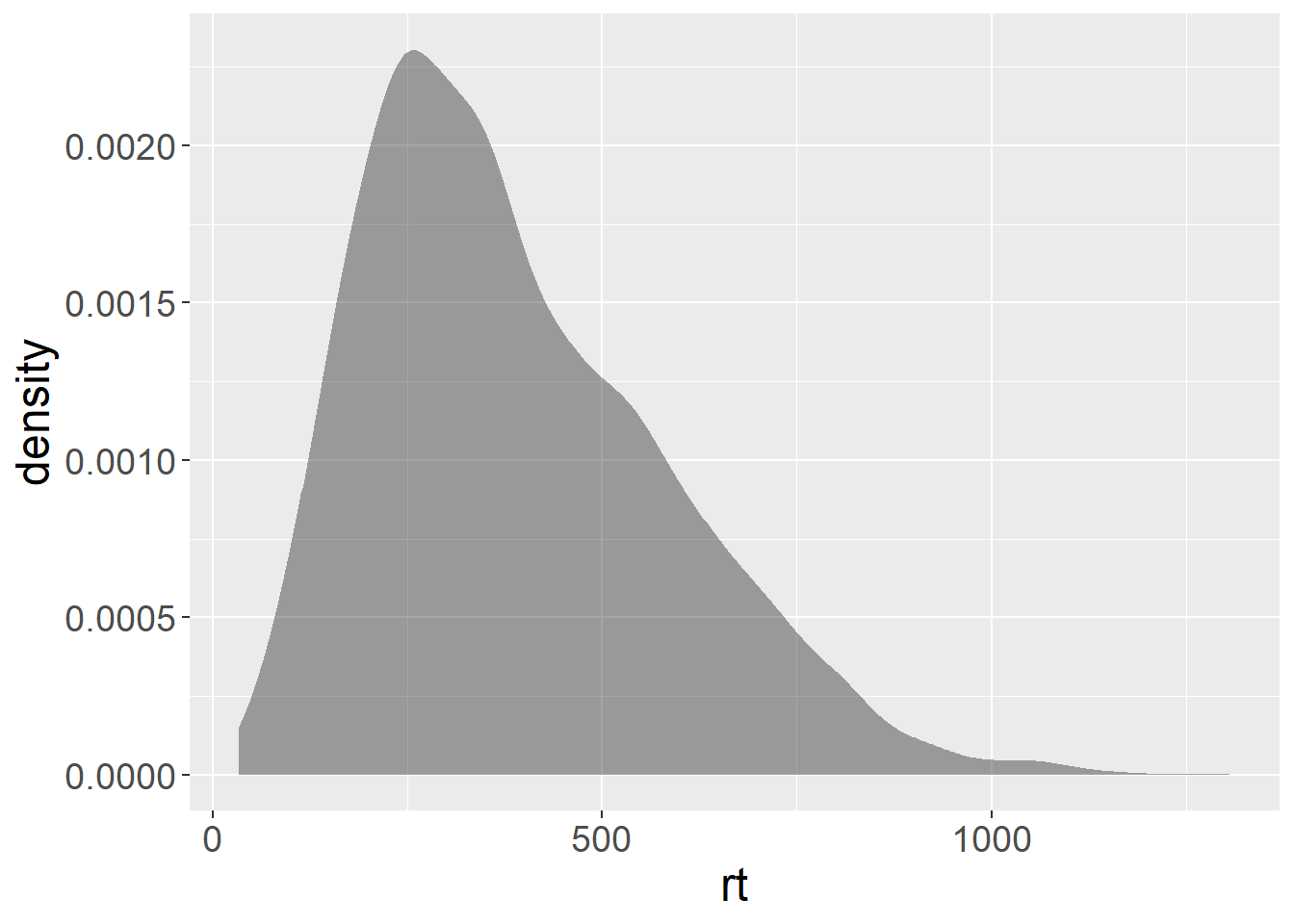

---

Analisi Statistica

Preparo il dataframe

Anzitutto mettiamo i dati osservati in un dataframe:

df = data.frame(id=as.factor(id), Distance, rt)
head(df)

  id Distance       rt
1  1        1 387.6420
2  1        1 412.9519
3  1        1 280.9995
4  1        1 386.3703
5  1        1 433.6993
6  1        1 455.0178

Fitting dei dati coi GAM

Fittiamo il modello gam con intercette e slope random, e la family Gamma con funzione legame logaritmo. Lo facciamo per quanto possibile, perché in realtà il mixed-model sarebbe idealmente implementato dalla funzione gamm(), che però al momento non supporta family diverse dalla Gaussian, quindi ci arrabattiamo in qualche modo con gam():

fit = gam(rt ~ s(Distance, k = 3) +
               s(id, bs = "re") + 
               s(Distance, id, bs = "fs", m = 1), 
    family = Gamma(link = "log") , 
    data = df)

Warning in gam.side(sm, X, tol = .Machine$double.eps^0.5): model has repeated
1-d smooths of same variable.

Abbiamo fissato la smoothing basis (bs) dei partecipanti come "re" che è descritta nel pacchetto come adatta per random effects distribuiti normalmente. Per la random slope (intesa come interazione Distance x id) abbiamo usato bs = "fs" descritti come efficienti quando c’è un gran numero di livelli e specialmente con l’uso dei gamm (mixed).

ypred = predict(fit)
ggplot(data.frame(),aes(x=df$Distance,y=exp(ypred),group=as.factor(df$id),color=as.factor(df$id)))+
  geom_line(size=1)+
  geom_point(size=3)+
  scale_x_continuous(breaks=1:ndistances)+
  theme(text=element_text(size=25))+
  labs(x="Distance",y="Expected RT",color="id")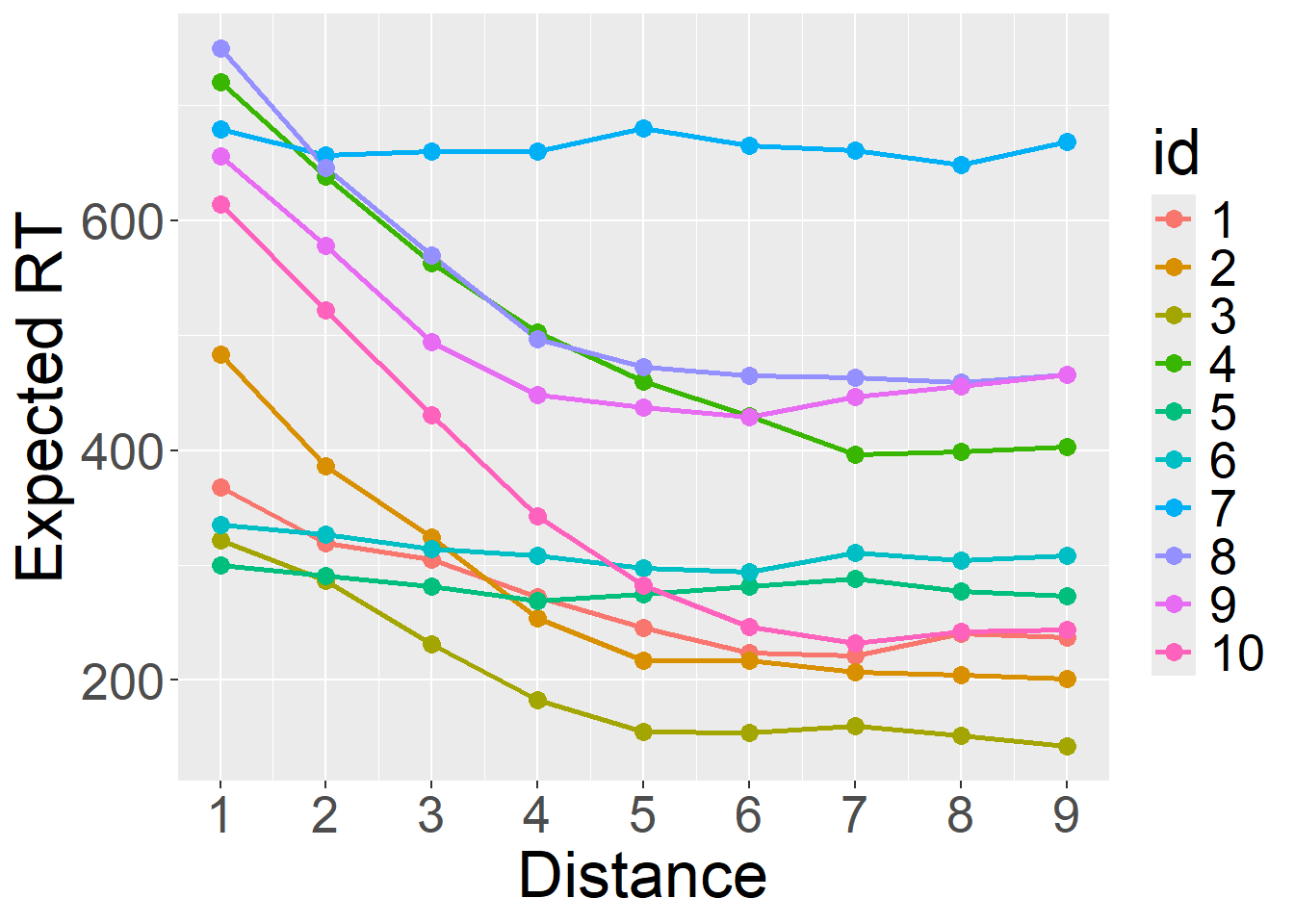

Test degli effetti?

Vediamo il summary del modello:

summary(fit)

Family: Gamma 
Link function: log 

Formula:
rt ~ s(Distance, k = 3) + s(id, bs = "re") + s(Distance, id, 
    bs = "fs", m = 1)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   5.8723     0.1482   39.62   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                  edf Ref.df        F p-value    
s(Distance)     1.880  1.904   56.382  <2e-16 ***
s(id)           4.495 10.000    0.629  <2e-16 ***
s(Distance,id) 46.521 88.000 6783.745   0.182    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.688   Deviance explained = 65.8%
GCV = 0.096206  Scale est. = 0.090897  n = 3600

La seguente tabella estrapolata dal summary, in particolare, ci offre dei test: 1) per l’effetto fisso generale di Distance; 2) per la varianza delle intercette random; 3) per la varianza delle slope random.

summary(fit)$s.table

                     edf    Ref.df            F   p-value
s(Distance)     1.879660  1.903602   56.3817616 0.0000000
s(id)           4.494829 10.000000    0.6291842 0.0000000
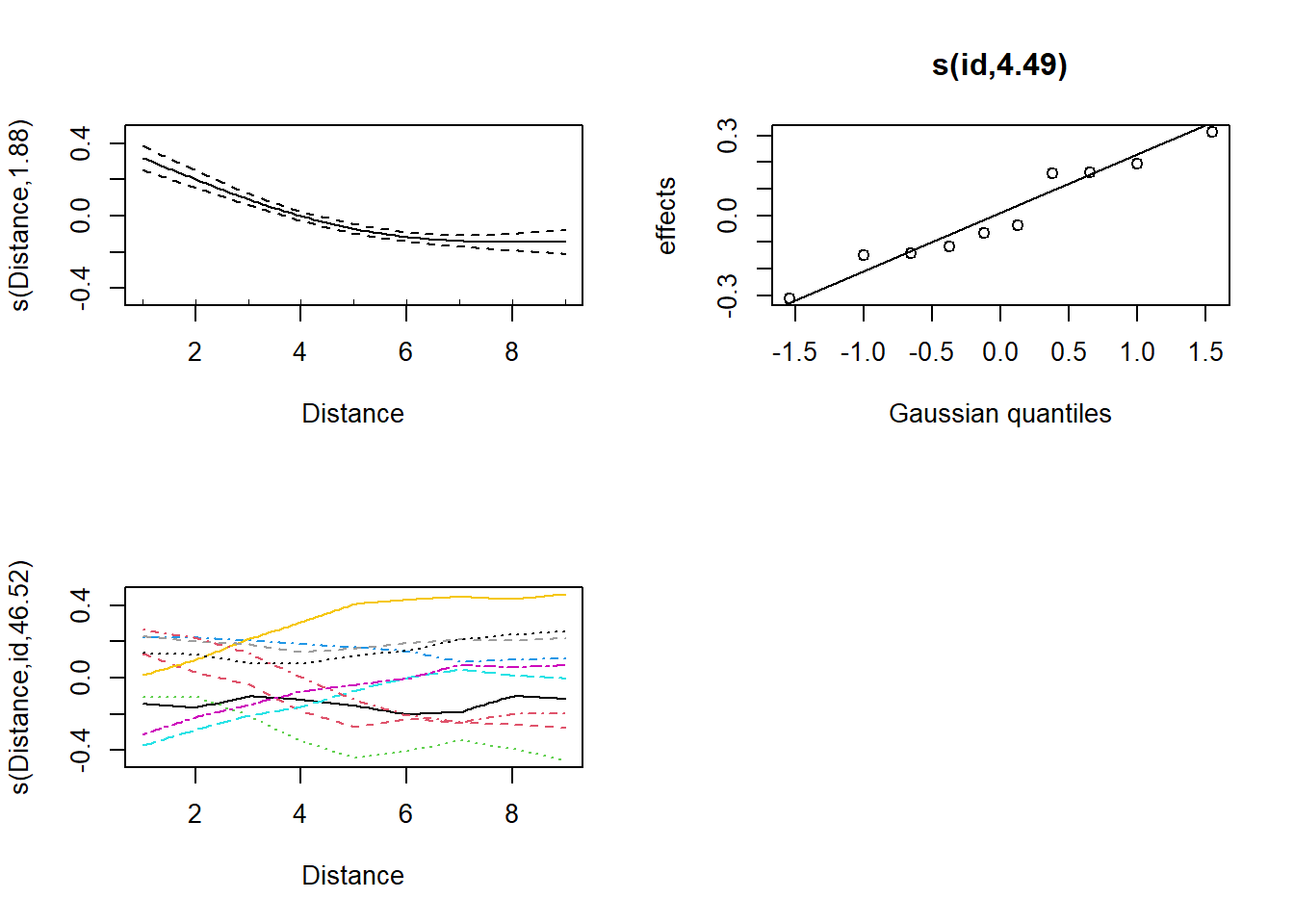
s(Distance,id) 46.520616 88.000000 6783.7446934 0.1815236

Contrariamente ai classici modelli lineari, con gli smoother non abbiamo un singolo trend lineare che è “significativamente positivo” o “significativamente negativo”. Un modo semplice per valutare se l’effetto principale di Distance (che è comunque “significativo”) è positivo, negativo, o un mix, è fare una visual inspection dell’effetto fisso principale:

plot(fit,pages=1)