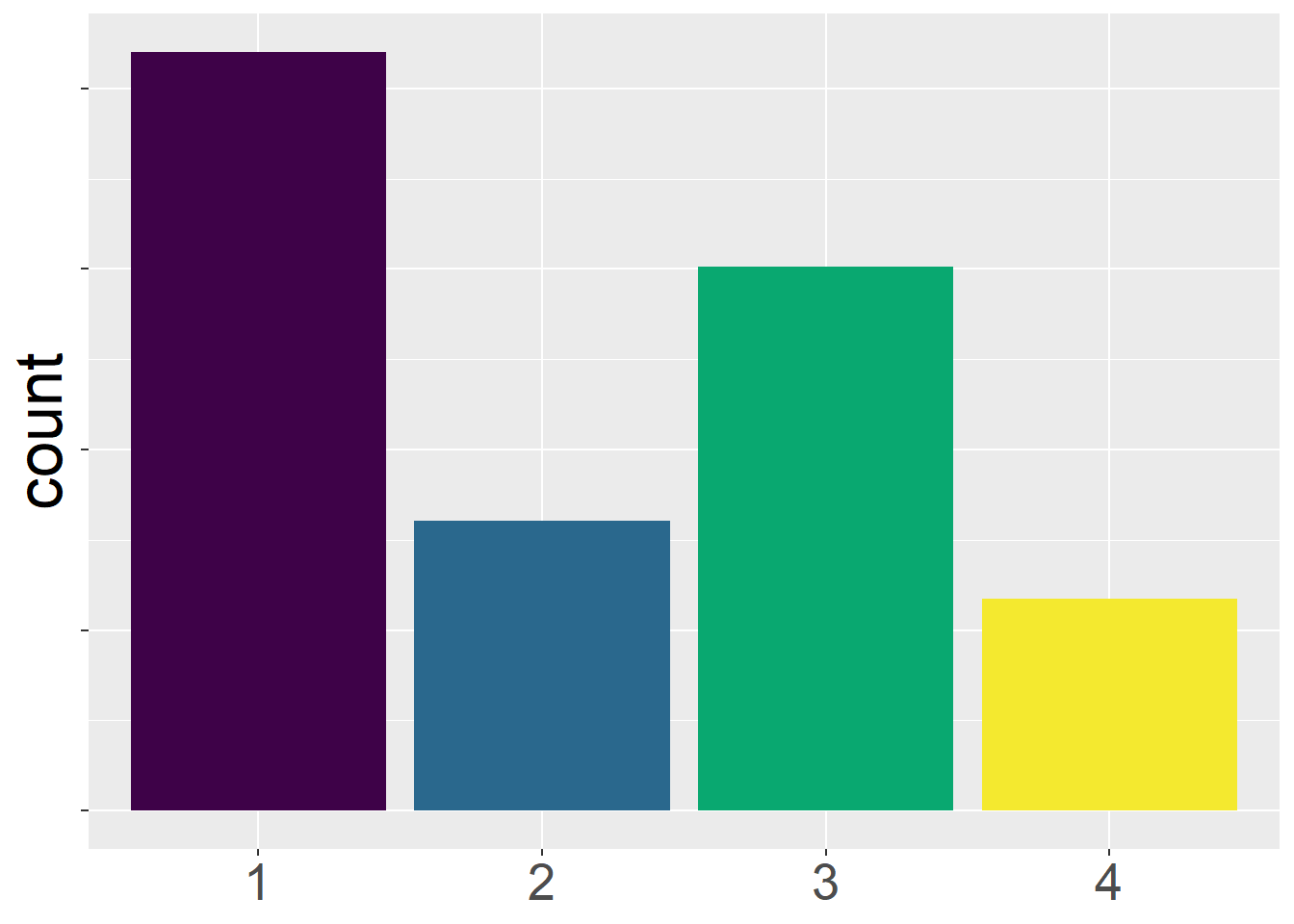
Alpha di Cronbach e dati ordinali
(torna alla prima parte sulle Basi dell’Alpha di Cronbach)
L’Alpha di Cronbach in realtà si usa quasi sempre per risposte a questionari con item su scala Likert.
Continuum e thresholds
Possiamo immaginare la risposta ordinale come una segmentazione su un certo numero di livelli ordinali di un continuo sottostante che può essere distribuito come una Gaussiana. In base a dei livelli di threshold, il continuo sottostante diventa una sequenza di risposte ordinali. Si veda la seguente figura copiata da Gambarota & Altoè (2024):
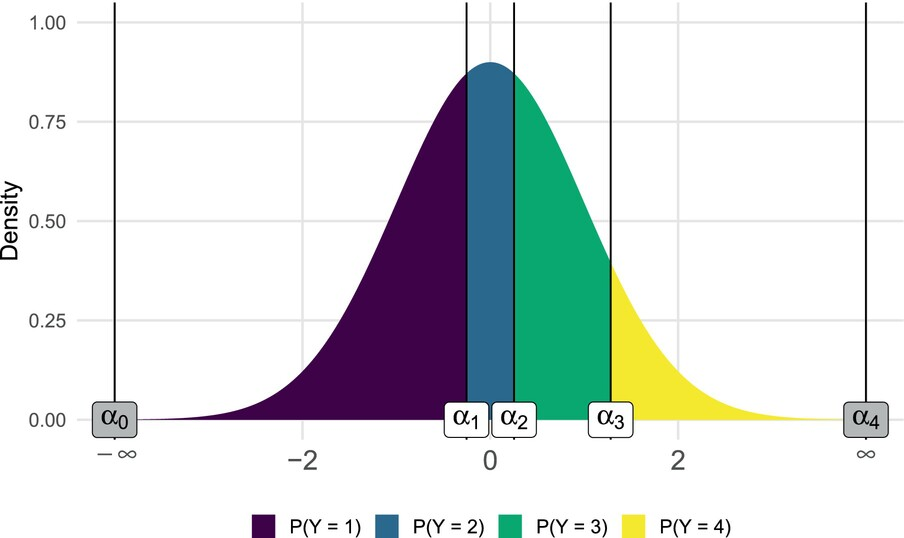
In base a questo continuum, potremmo aspettarci una distribuzione delle risposte di questo tipo:
Possiamo ignorare la natura ordinale degli item?
Possiamo utilizzare il semplice Alpha di Cronbach, così com’è, anche sui dati ordinali? Poniamo che quelle sopra siano davvero le thresholds. Poniamo di avere k = 5 item con un continuum sottostante variamente correlato (vedi figura sotto).
Come si vede dal grafico, anche trascurando del tutto la natura ordinale degli item, apparentemente l’Alpha di Cronbach non va così male: sovrastima un po’ per i valori più alti, ma riflette abbastanza bene l’effettiva correlazione tra il Sum score dei dati ordinali e il Vero tratto latente.
Show the code
library(lavaan)
library(psych)
meanLoad = seq(.4,1.2,length.out=20)
res1 = data.frame(meanLoad=meanLoad,
meanCorr=NA,
AlphaCronbach=NA,
AlphaCronbachPolyc=NA,
VarVera=NA,
VarOrd=NA)
for(i in 1:nrow(res1)){
N = 1e5
X_true = rnorm(N,0,1)
X1 = scale(res1$meanLoad[i]*X_true + rnorm(N,0,1))
X2 = scale(res1$meanLoad[i]*X_true + rnorm(N,0,1))
X3 = scale(res1$meanLoad[i]*X_true + rnorm(N,0,1))
X4 = scale(res1$meanLoad[i]*X_true + rnorm(N,0,1))
X5 = scale(res1$meanLoad[i]*X_true + rnorm(N,0,1))
res1$VarVera[i] = cor(rowSums(cbind(X1,X2,X3,X4,X5)),X_true)^2
x1 = as.numeric(cut(X1,breaks=c(-Inf,-0.2,0.2,1.2,Inf),labels=c(1,2,3,4)))
x2 = as.numeric(cut(X2,breaks=c(-Inf,-0.2,0.2,1.2,Inf),labels=c(1,2,3,4)))
x3 = as.numeric(cut(X3,breaks=c(-Inf,-0.2,0.2,1.2,Inf),labels=c(1,2,3,4)))
x4 = as.numeric(cut(X4,breaks=c(-Inf,-0.2,0.2,1.2,Inf),labels=c(1,2,3,4)))
x5 = as.numeric(cut(X5,breaks=c(-Inf,-0.2,0.2,1.2,Inf),labels=c(1,2,3,4)))
res1$VarOrd[i] = cor(rowSums(cbind(x1,x2,x3,x4,x5)),X_true)^2
df = data.frame(x1,x2,x3,x4,x5)
res1$meanCorr[i] = mean(cor(df)[lower.tri(cor(df))])
#model = "X_latent =~ x1+x2+x3+x4+x5"
#fit = cfa(model, df)
res1$AlphaCronbach[i] = psych::alpha(df)$total$raw_alpha
res1$AlphaCronbachPolyc[i] = alpha(polychoric(df)$rho)$total$raw_alpha
}Show the code
ggplot(res1,aes(x=VarOrd,y=AlphaCronbach,color=meanCorr))+
geom_abline(slope = 1, intercept = 0, linetype = "dashed", size=1)+
scale_color_gradient(low = "deepskyblue", high = "blue4")+
geom_point(size=6,alpha=.8)+
theme(text=element_text(size=20))+
xlab("Correlazione ^2 \n (Sum score ordinale e Tratto latente)")+
ylab("Alpha di Cronbach 'ignorante'")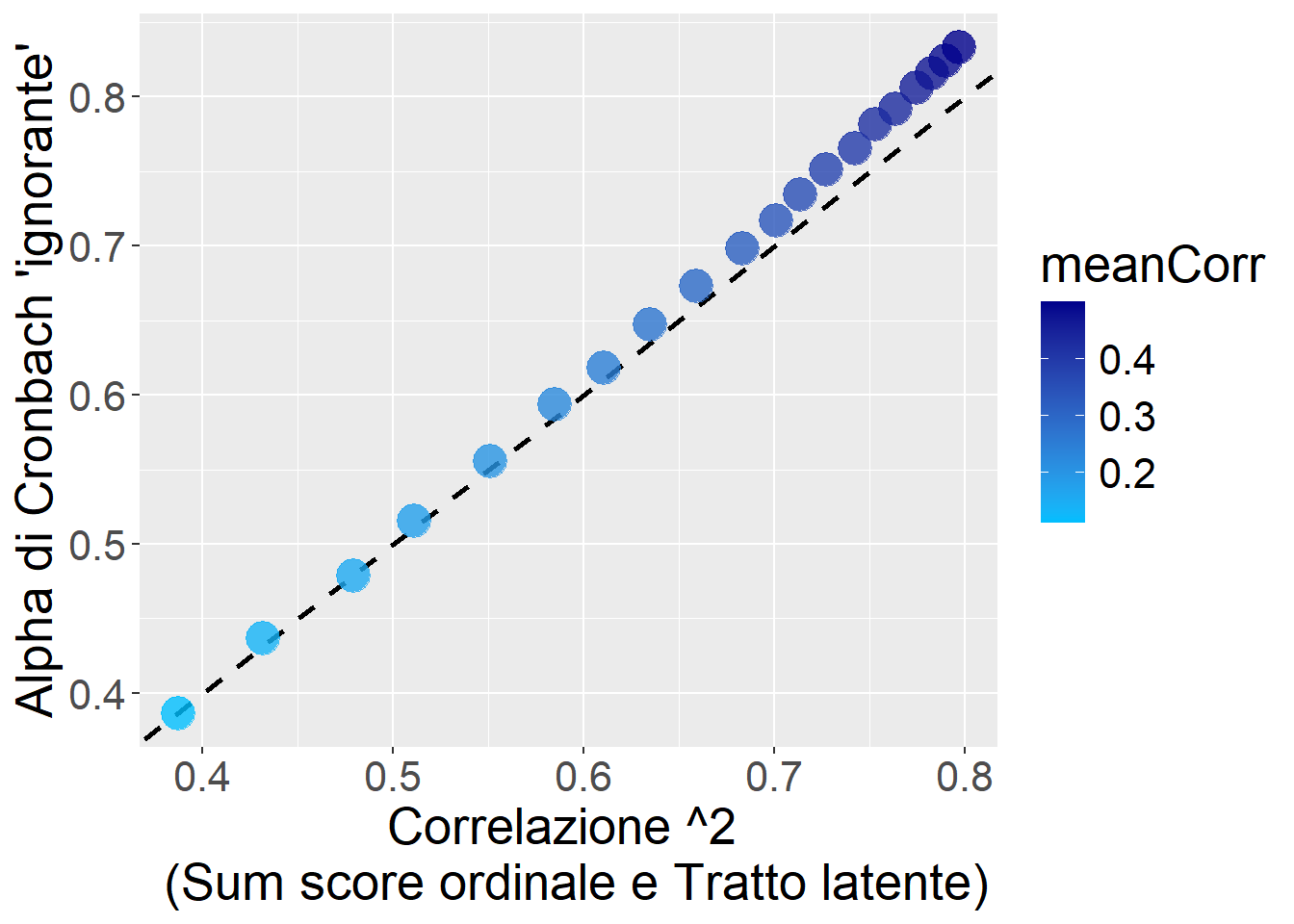
TUTTAVIA quella qui sopra è comunque, complessivamente, una sottostima del vero “potenziale” di attendibilità se trattassimo e gestissimo i dati ordinali come tali.
La seguente figura mostra l’Alpha di Cronbach calcolato prima in funzione della vera correlazione tra il Sum score originale (del continuum sottostante, cioè prima di essere reso ordinale) e il vero tratto latente:
Show the code
ggplot(res1,aes(x=VarVera,y=AlphaCronbach,color=meanCorr))+
geom_abline(slope = 1, intercept = 0, linetype = "dashed", size=1)+
scale_color_gradient(low = "deepskyblue", high = "blue4")+
geom_point(size=6,alpha=.8)+
theme(text=element_text(size=20))+
xlab("Correlazione ^2 \n (Sum score continuum sottostante \n e Tratto latente)")+
ylab("Alpha di Cronbach 'ignorante'")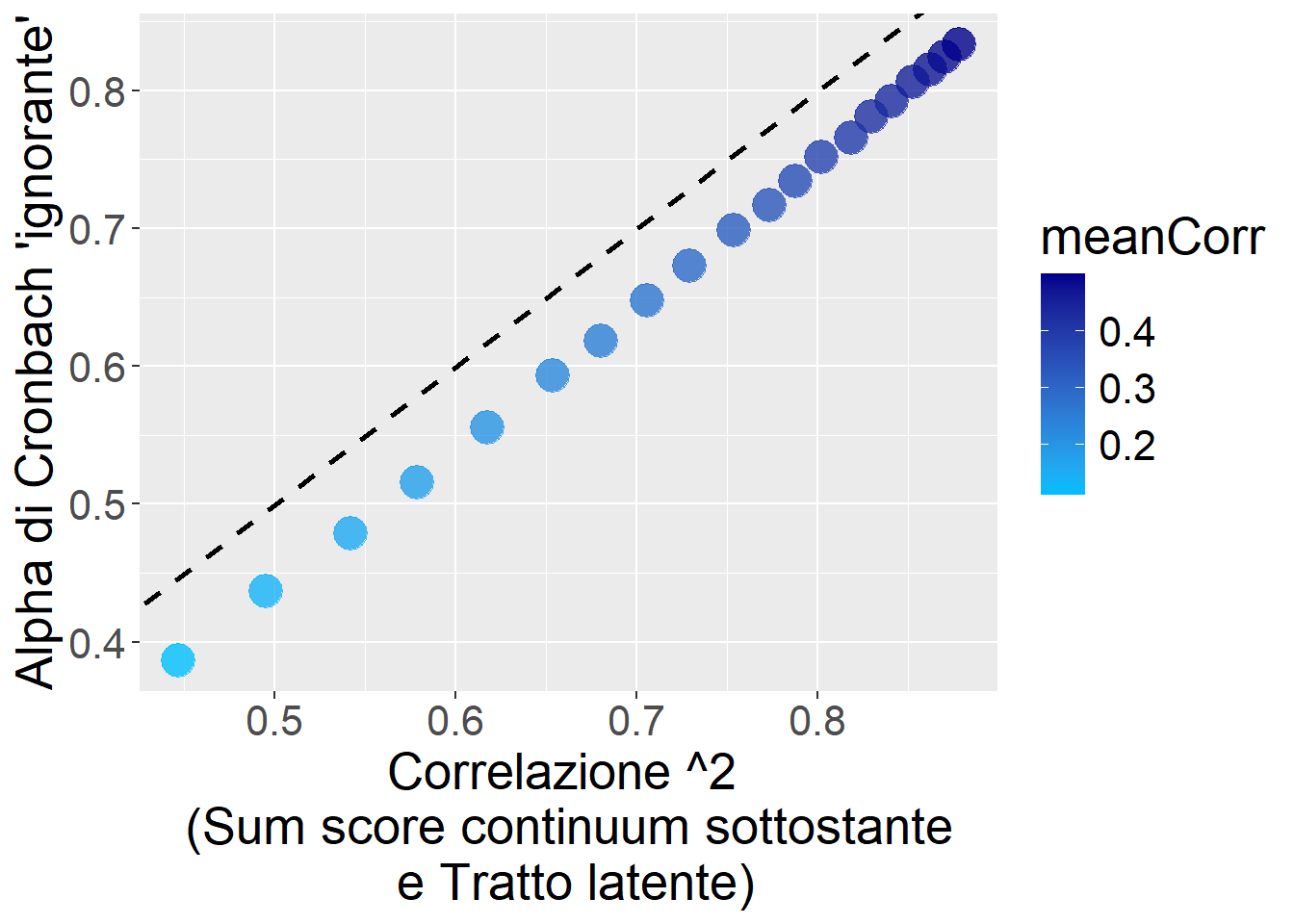
E le correlazioni policoriche?
Un’opzione spesso usata è calcolare l’Alpha di Cronbach usando le correlazioni policoriche tra i dati ordinali.
# Esempio calcolo Alpha con correlazioni policoriche
library(psych)
rho = polychoric(df)$rho
alpha(rho)$total raw_alpha std.alpha G6(smc) average_r S/N median_r
0.8767998 0.8767998 0.8506103 0.5873523 7.116873 0.5873429Funziona!
Questo Alpha di Cronbach coglie bene la correlazione tra il Sum score del continuum sottostante (nella realtà non osservato) e il Vero tratto latente (con il Factor score è più o meno lo stesso, tuttavia per tempi computazionali non ho provato il Factor score con ordered=TRUE).
ggplot(res1,aes(x=VarVera,y=AlphaCronbachPolyc,color=meanCorr))+
geom_abline(slope = 1, intercept = 0, linetype = "dashed", size=1)+
scale_color_gradient(low = "deepskyblue", high = "blue4")+
geom_point(size=6,alpha=.8)+
theme(text=element_text(size=20))+
xlab("Correlazione ^2 \n (Sum score continuum sottostante \n e Tratto latente)")+
ylab("Alpha di Cronbach 'Polychoric'")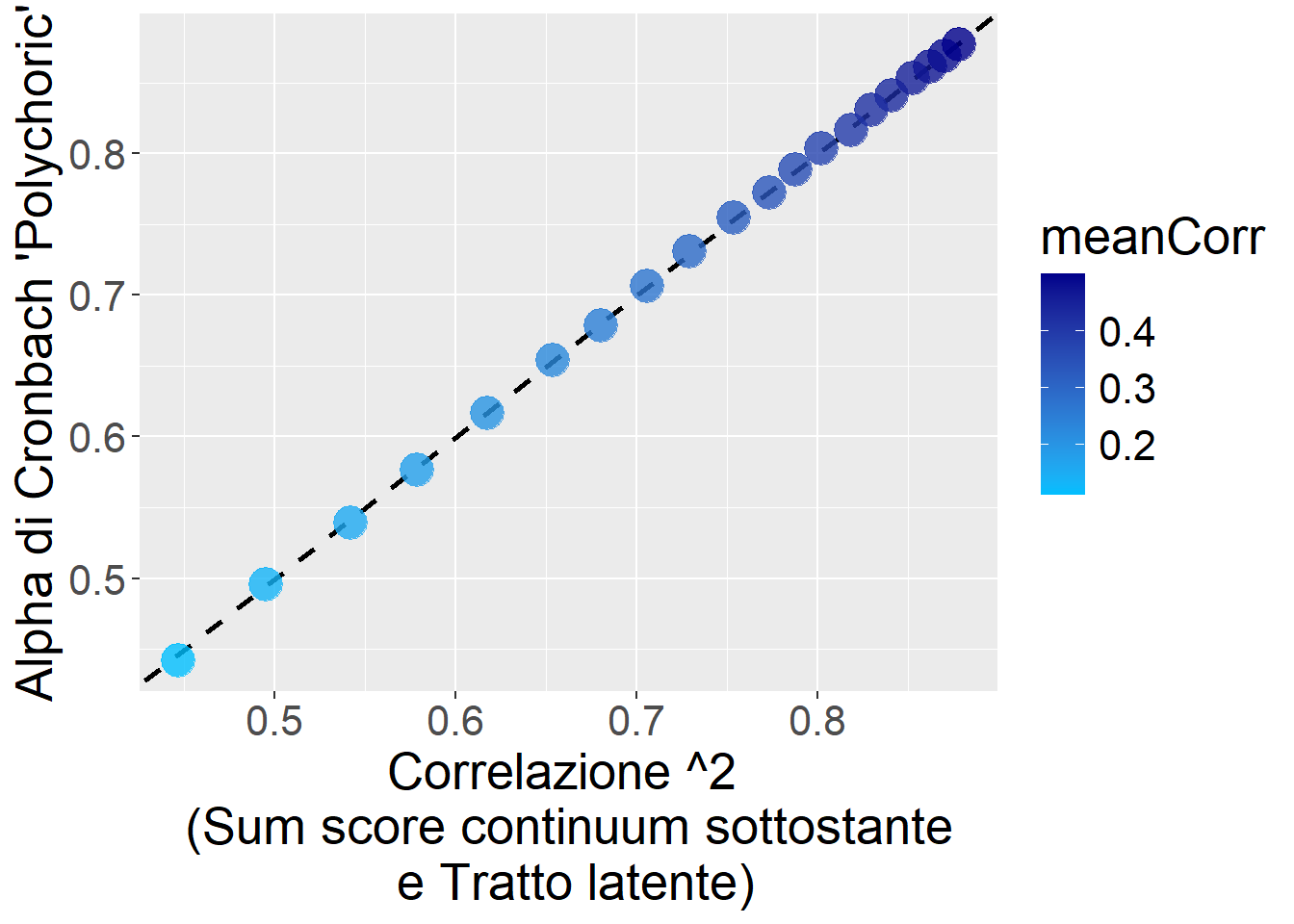
Però ATTENZIONE: questo Alpha di Cronbach Policorico è informativo SOLO se poi trattiamo gli item come realmente ordinali, ad esempio con un modello SEM specificando ordered=TRUE, altrimenti, se poi facciamo il semplice Sum score dei dati ordinali, allora l’attendibilità di quest’ultimo NON è quella suggerita dall’Alpha di Cronbach Policorico, ma più bassa.
C’è un altro modo di calcolare l’Alpha ordinale?
Possiamo utilizzare il pacchetto semTools sulle CFA per dati ordinali fittate col pacchetto lavaan. Fare le CFA è sempre raccomandato! Ecco un esempio.
Show the code
# Simulazione dati
set.seed(0)
N = 1500
X_true = rnorm(N,0,1)
X1 = scale(0.8*X_true + rnorm(N,0,1))
X2 = scale(0.8*X_true + rnorm(N,0,1))
X3 = scale(0.8*X_true + rnorm(N,0,1))
X4 = scale(0.8*X_true + rnorm(N,0,1))
X5 = scale(0.8*X_true + rnorm(N,0,1))
df = data.frame(
x1 = as.numeric(cut(X1,breaks=c(-Inf,-0.2,0.2,1.2,Inf),labels=c(1,2,3,4))),
x2 = as.numeric(cut(X2,breaks=c(-Inf,-0.2,0.2,1.2,Inf),labels=c(1,2,3,4))),
x3 = as.numeric(cut(X3,breaks=c(-Inf,-0.2,0.2,1.2,Inf),labels=c(1,2,3,4))),
x4 = as.numeric(cut(X4,breaks=c(-Inf,-0.2,0.2,1.2,Inf),labels=c(1,2,3,4))),
x5 = as.numeric(cut(X5,breaks=c(-Inf,-0.2,0.2,1.2,Inf),labels=c(1,2,3,4)))
)library(lavaan)
model = "
X_latent =~ x1+x2+x3+x4+x5
"
fit = cfa(model, df, ordered=T)
library(semTools)
reliability(fit) X_latent
alpha 0.7119877
alpha.ord 0.7670069
omega 0.7115317
omega2 0.7115317
omega3 0.7116592
avevar 0.3974567# compRelSEM(fit) # in questo caso ci restituisce l'omegaper controprova vediamo se coincide con l’Alpha calcolato sulle correlazioni policoriche:
library(psych)
alpha(polychoric(df)$rho)$total raw_alpha std.alpha G6(smc) average_r S/N median_r
0.7670009 0.7670009 0.7264698 0.3969991 3.291862 0.3888338